一个奇思妙想，欢迎交流！

太长不看版

对于从 $(x_0, 0)$ 运动到 $(x_1, 0)$、每帧横坐标增加 $p \cdot (x_1 - x)$ 的非线性运动，角色横坐标 $x$ 和时间（经过的帧数）$t$ 之间有：

$$x(t) = (x_1-x_0)\cdot(p-1)\cdot(1-p)^{t-1}+x_1$$

以从 $(0, 0)$ 运动到 $(100, 0)$、每帧横坐标增加 $\frac{100 - x}{10}$ 为例：

$$x(t) = -90 \cdot (\frac{9}{10})^{t-1} + 100$$

介绍

在动画中合理的使用非线性移动可以使动画看起来更加自然、舒适。在 Scratch 中最常用的非线性移动（之一）是这样的：

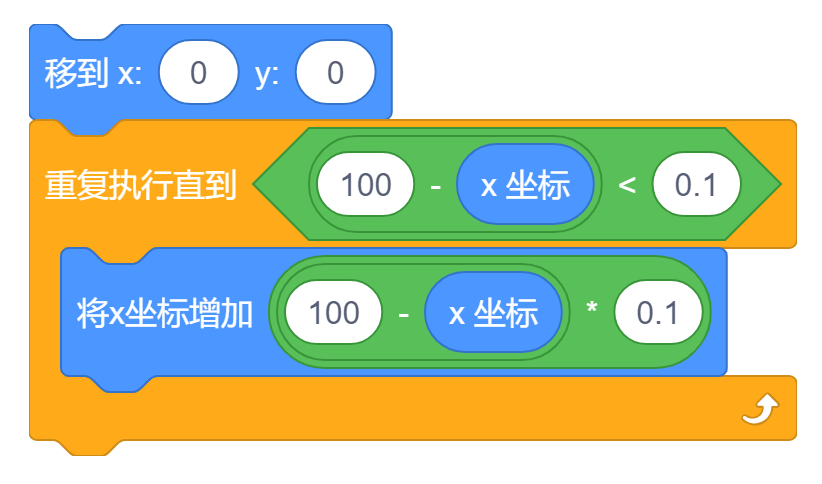
我们以上图所展示的运动为例，角色从 $(0, 0)$ 位置非线性的移动到了 $(100, 0)$ 的位置，每帧（每次循环）都会使横坐标增加 $\frac{100 - x}{10}$，因此距离目标位置越远运动速度越快、越近运动速度越慢，是一种非线性运动.
下面我们将探究角色横坐标 $x$ 随时间 $t$ 变化而变化的规律.

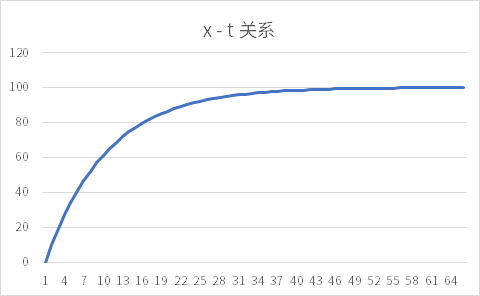
推导

我们规定第一帧（经过一次循环）时 $t = 1$、第两帧时为 $t = 2$ ......

以上面提到的非线性运动为例，如果 $t = n$ 时角色的横坐标 $x$ 为 $a_n$，则：

$$a_1 = 0 + \frac{100 - 0}{10} = 10 \\$$

$$a_n = a_{n-1} + \frac{100 - a_{n-1}}{10} = \frac{9}{10} a_{n-1} + 10$$

如果通项公式形如 $a_{n} = A \cdot a_{n-1} + B$（$A, B \in R$），我们可以构造等比数列：

$$对于 \ a_{n} = A \cdot a_{n-1} + B\\ \therefore a_{n} = q \cdot a_{n-1} + (q - 1) \cdot t\\ \therefore a_n + t = q \cdot ( a_{n-1} + t ) \\ \therefore \frac{a_n + t}{a_{n-1} + t} = q \\ 可得公比为 \ q \ 的等比数列 \ \{a_n + t\}$$

$$\therefore a_n = \frac{9}{10} \cdot a_{n-1} + (\frac{9}{10} - 1) \cdot (-100) \\[0.5em] \therefore a_n - 100 = \frac{9}{10} \cdot (a_{n-1} -100) \\[0.5em] \therefore \frac{a_n - 100}{a_{n-1} - 100} = \frac{9}{10}$$

现在我们得到了一个公比为 $\frac{9}{10}$ 的等比数列 $\{a_n - 100\}$.

$$\because a_1 = 10 \\ \therefore a_1 - 100 = -90$$

数列 $\{a_n - 100\}$ 的首项为 $-90$，我们可以得到它的通项公式：

$$a_n - 100 = -90 \cdot (\frac{9}{10})^{n-1}$$

因此：

$$a_n = -90 \cdot (\frac{9}{10})^{n-1} + 100$$

所以对于这种情况，$x(t) = -90 \cdot (\frac{9}{10})^{t-1} + 100$.

更进一步，对于从 $(x_0, 0)$ 运动到 $(x_1, 0)$、每帧横坐标增加 $p \cdot (x_1 - x)$ 的非线性运动，有：

$$a_1 = x_0 + p \cdot (x_1 - x_0) \\ \begin{align*} a_n &= a_{n-1} + p \cdot (x_1 - a_{n-1}) \\ &= (1-p) \cdot a_{n-1} + p \cdot x_1 \end{align*}$$

因此：

$$\begin{align} & \therefore q = 1-p, \ t = \frac{p \cdot x_1}{1-p-1}=-x_1 \\ & \therefore \frac{a_n - x_1}{a_{n-1} - x_1} = 1-p \\ & \begin{align*} \therefore a_1 - x_1 &= x_0 - x_1 + p \cdot (x_1 - x_0) \\ &= (x_1 - x_0) \cdot (p - 1) \\ \end{align*} \\ & \therefore a_n - x_1 = (x_1 - x_0) \cdot (p - 1) \cdot(1-p)^{t-1} \\ & \therefore x(t) = (x_1-x_0)\cdot(p-1)\cdot(1-p)^{t-1}+x_1 \end{align}$$

使用表格验证，符合预期：