一点思考,欢迎指正错误、提出建议!
必修二中,我们学习过 运动的合成与分解 这一课,课本指出:
运动的合成与分解遵从矢量运算法则。
并且我们也学习了合运动和分运动间具有 等效性(各分运动叠加的效果与合运动相同)、独立性(分运动间相互独立、互不干扰)和 等时性(合运动和分运动同时开始与结束)。
在 2024 年北京市朝阳区一模第 20 题中,就出现了基于运动的合成与分解的考察(配速法):
根据牛顿力学经典理论,只要物体的初始条件和受力情况确定,就可以推知物体此后的运动情况。
情境 1:如图 1 所示,空间存在水平方向的匀强磁场(垂直纸面向里),磁感应强度大小为 B,在磁场中 M 点处有一质量为 m、电荷量为 +q 的带电粒子。已知重力加速度 g。
(1)若使带电粒子获得某一水平向右的初速度,恰好作匀速直线运动,求该速度的大小 ;
(2)若在 M 点静止释放该粒子,其运动将比较复杂。为了研究该粒子的运动,可以应用运动的合成与分解的方法,将它为零的初速度分解为大小相等的水平向左和水平向右的速度。求粒子运动过程中的最大速率。
......
在 (1) 中,粒子受到向下的重力 和向上的洛伦兹力 ,当二者平衡时、它做匀速直线运动,有 .
(2) 中,题目提示我们 “可以应用运动的合成与分解的方法,将它为零的初速度分解为大小相等的水平向左和水平向右的速度”,并且 (1) 中也提醒我们,当速度 时,粒子做匀速直线运动,因此我们可以:
-
将粒子的速度分解为向左、向右的两个速度,大小均为 .
-
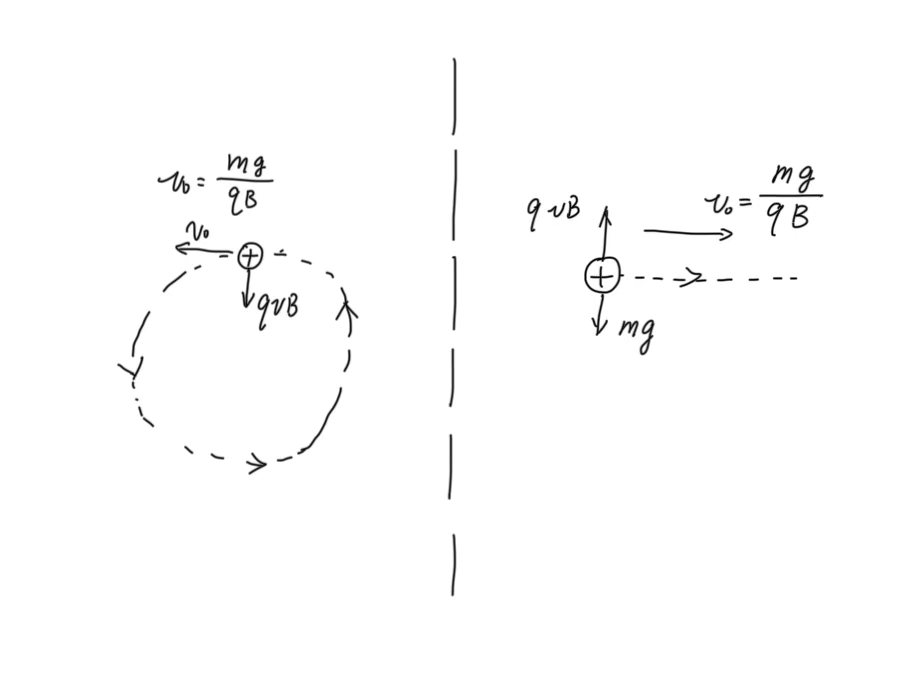
- 其中 向右的速度 在 洛伦兹力 和 重力 (二力平衡)的作用下,做 匀速直线运动、速度大小为 .(如下图右侧)
- 向左的速度 在 洛伦兹力 的作用下,做 匀速圆周运动、速度大小为 .(如下图左侧)
-
当左右两个运动速度均向右时,其合成的运动速度最大,大小为 ,即 .
但是我们发现,两个分运动都各自具有一个洛伦兹力,但是合运动却只有一个洛伦兹力,所以说在分解合运动的时候,我们是让洛伦兹力凭空增加了一个吗?
其实不然,我们可以理解为“在磁场中有速度就有洛伦兹力”,分运动具有速度、而且他们也有“独立性”,所以各自一定会有洛伦兹力,分运动的两个洛伦兹力之矢量和与合运动的一个洛伦兹力是相等的。
类似地,如果把“弹簧拉着小球做圆周运动”正交分解成了两个“弹簧拉着小球做简谐运动”的分运动,其中弹簧的弹力是“有‘位移’就有弹力”,因此两个分运动具有两个弹力。
但是重力是恒定的,它不因位移或者速度的改变而发生变化,所以分解时不能“一个分运动一个重力 ”。
在运动的分解与合成中,我们应该把握对位移 / 速度 / 加速度(力)这三个矢量的分解与合成。例如,物体合运动的位移等于各个分运动位移的矢量和。
在这道题中,我们就可以借助这样的思想分析粒子的运动位移(轨迹):
(以初始位置为原点,当时间 时)
- 分运动 匀速直线运动 的位移 .
- 分运动 匀速圆周运动 的位移 .
- 合运动的位移 .